Big Data Management Exercises
Principle in Data Science Exercises
Data Analytics Exercises
Data Mining Exercises
Network Security Exercises
Other Exercises:
Python String Exercises
Python List Exercises
Python Library Exercises
Python Sets Exercises
Python Array Exercises
Python Condition Statement Exercises
Python Lambda Exercises
Python Function Exercises
Python File Input Output Exercises
Python Tkinter Exercises
Big Data - Exercises 2
21. What are the differences among structured, unstructured and semi-structured datasets forms in Big Data? Explain and provide examples of data.Ans:

22. Provide different types of data analytics. What are the objectives of these different types of analytics?
Ans:

23. For Data Intensive Scalable Computing: Simply processing large datasets is typically not considered to be big data. Groups like Conseil Européen pour la Recherche Nucléaire (CERN) and Transnational Research In Oncology (TRIO) have been using High Performance Computing systems and scalable software to analyze very large datasets.
However, this is considered compute-centric processing. Typically, a mathematical algorithm is used to generate results from the data that forms the input. This is true for computational fluid dynamics, image processing, and traditional genome analysis.
Try to research and find out the salient differences between “big compute systems” and “big data systems” that utilizes data intensive scalable computing technologies.
Ans:

24a. what would be the number of suspected pairs based on the following condition?
Condition:
A pair of people, and a pair of days, such that two people are at the same hotel on each of two days.
Two people at the same hotel on each of two days
109 people being tracked.
1000 days.
Each person stays in a hotel 1% of the time (10 days out of 1000).
Hotels hold 100 people (so 105 hotels).
Ans:
1 x 10^9 that might be evil doers
• Everyone has a 10^-2 chance of going to a hotel on a single day
• 1 x 10^7 going to hotels 1 hotel can accommodate 100 people, i.e. 10^2
Therefore, there shall be 10^5 hotels
Probability of two people going to hotel at any given day = 1/100 x 1/100 = 10^-4
Chances of two people visiting the same hotel at any given day = 10^-4 / 10^5 = 10^-9
Chance of visiting the same hotel on a different day = 10^-9 x 10^-9 = 10 ^-18
ASSUMPTION TO SIMPLIFY ARITHMETIC:
• For large n, n C 2= n 2/2
A pair of people
Probability to have a pair of people: 10^9C2 = 5 x 10^17
A pair of days
Probability for a pair of days = 1000C2 = 5 x 10^5
Therefore, the final answer of probable people looking like evil doers would be = (5 x 10^17) x (5 x 10^5) x (10 ^-18) = 250,000
24b. what would be the number of suspected pairs if the following changes were made to the data (and all other numbers remained as they were in the previous section)?
- The number of days of observation was raised to 2000.
Ans:
Two people at the same hotel on each of two days
Does not change, unaffected by the number of days we observe the record
10 ^-18
A pair of people
Does not change, unaffected by the number of days we observe the record
5 x 10^17
A pair of days
Probability for a pair of days = 2000C2 = 2 x 10^6
Therefore, the final answer of probable people looking like evil doers would be = (5 x 10^17) x (2 x 10^6) x (10 ^-18) = 10^6
24c. what would be the number of suspected pairs if the following changes were made to the data (and all other numbers remained as they were in the previous section)?
- The number of people observed was raised to 2 billion (and there were therefore 200,000 hotels).
Ans:
Two people at the same hotel on each of two days
2 x 10^9 that might be evil doers
• Everyone has a 10^-2 chance of going to a hotel on a single day
• 2 x 10^7 going to hotels
1 hotel can accommodate 100 people, i.e. 10^2
Therefore, there shall be 2 x 10^5 hotels
Probability of two people going to hotel at any given day = 1/100 x 1/100 = 10^-4
Chances of two people visiting the same hotel at any given day = 10^-4 / (2 x 10^5) = 5 x 10^-10
Chance of visiting the same hotel on a different day = 10^-9 x 10^-9 = 2.5 x 10 ^-19
A pair of people
Probability to have a pair of people: 2x10^9C2 = 2 x 10^18
A pair of days
Does not change, unaffected by number of people observed
5 x 10^5
Therefore, the final answer of probable people looking like evil doers would be =
(2 x 10^18) x (5 x 10^5) x (2.5 x 10^-19) = 250,000
24d. what would be the number of suspected pairs if the following changes were made to the data (and all other numbers remained as they were in the previous section)?
- We only reported a pair as suspect if they were at the same hotel at the same time on three different days.
Ans:
Two people at the same hotel on each of three days
1 x 10^9 that might be evil doers
• Everyone has a 10^-2 chance of going to a hotel on a single day
• 1 x 10^7 going to hotels
1 hotel can accommodate 100 people, i.e. 10^2
Therefore, there shall be 10^5 hotels
Probability of two people going to hotel at any given day = 1/100 x 1/100 = 10^-4
Chances of two people visiting the same hotel at any given day = 10^-4 / 10^5 = 10^-9
Chance of visiting the same hotel on each of three days = 10^-9 x 10^-9 x 10^-9 = 10 ^-27
A pair of people
Does not change.
10^9C2 = 5 x 10^17
Three different days
Probability for three different days = 1000C3 = 166,167,000
Therefore, the final answer of probable people looking like evil doers would be =
(5 x 10^17) x 166,167,000 x 10 ^-27 = 0.0831
25. What are the main components of Hadoop framework, and what is the main assumption in which Hadoop is built on?
Ans:
The main components of Hadoop framework are Hadoop common, Hadoop distributed file system (HDFS), Hadoop YARN, Hadoop Mapreduce. The elaboration of these components are listed below:
- Hadoop Common: Utilities that are used by the other modules.
- Hadoop Distributed File System (HDFS): A distributed file system like the one developed by Google under the name GFS.
- Hadoop YARN: This module provides the job scheduling resources used by the MapReduce framework.
- Hadoop MapReduce: A framework designed to process huge amount of data
The main assumption in which Hadoop is built on is hardware failure are common and should be automatically handled by the framework.
26. What are the main reasons that we need a distributed file system (DFS)? Justify your answer via a suitable example.
Ans:
The needs of distributed file system (DFS) are due to the explosive of data in recent year. Hence, conventional type of file system cannot support or process big data. So distributed file system is built to support these large files or big data from various sources. For instance, google has crawled 10 billion web pages with average size of 20KB for each webpage, hence it is about 200TB size. However, assuming the classical computational model can only be used in which all data resides on a single disc. Hence the fundamental limitation is limited by the data bandwidth between the disk and CPU.
27. What are commodity clusters, and what is its relationship with the cluster architecture?
Ans:
Commodity cluster is an ensemble of fully independent computing systems integrated by a commodity off-the-shelf interconnection communication network. Clusters represent more than 80% of all the systems on the Top 500 list and a larger part of commercial scalable systems. A single computer on a commodity cluster possesses normal specification and is not a supercomputer.
In cluster architecture, the servers/ nodes are contained within racks that each contain 16 – 64 nodes. They are further connected switches between racks, and further connected by backbone switches between switches for the individual racks. All of these nodes are considered residing on commodity clusters that have normal/ standard specifications that can be used for distributed processing.
28. How does DFS & Map Reduce solves the issues related to conventional computing architecture in handling big data?
Ans:
DFS and MapReduce attempts to solve 3 problems
• How to store data persistently and making it available if nodes fail, and dealing with nodes failures during long running computation
o By storing data in a distributed fashion across multiple nodes and multiple racks
• How to deal with network bottleneck?
o By bringing the computing nearer to the data
• Distributed processing model that is complicated (and involves a lot of parallel processing)
o By providing an environment that takes care of the distributed processing model automatically, and instead a user is only required to focus on solving a particular problem in a distributed manner via the usage of mappers and reducers.
29. Explain in your own words the roles of Chunk Servers, Master Node and a Client, within the Hadoop framework.
Ans:
Chunk server: A chunk server is the core engine who coordinate with master server. The request data chunks are sent to the client with the help of chunk servers. It tries to keep replicas in different racks.
Master Node: Master node in charge of coordination during MapReduce processes. It stores metadata.
Client: A computer or applications which creating new files or editing existing file on the system. It talks to master node to find chunk servers.
30. How are the problem solved for the followings:
a. How to store data persistently and keep it available if nodes fail?
Ans:
To store data redundantly on multiple nodes can ensure data persistently.
b. How to deal with node failures during a long running computation?
Ans:
To store the data redundantly on multiple nodes when encounters node failures, the replica data in another node can restart the computation.
31. How does the Hadoop framework deal with network bottleneck?
Ans:
Move computation close to data to minimize data movement.
32. Explain the Map-Reduce algorithm with the help of the Word Count problem.
Ans:
Let us understand, how a MapReduce works by taking an example where I have a text file called example.txt whose contents are as follows:
Dear, Bear, River, Car, Car, River, Deer, Car and Bear
Now, suppose, we have to perform a word count on the sample.txt using MapReduce. So, we will be finding the unique words and the number of occurrences of those unique words.
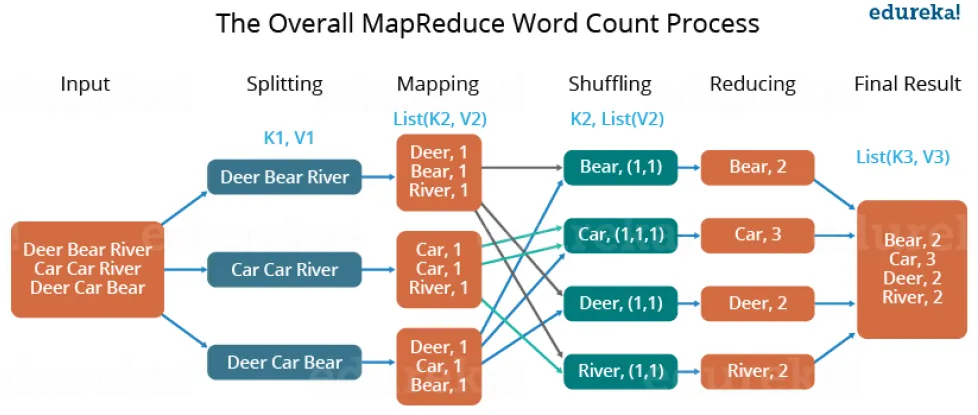
• First, we divide the input into three splits as shown in the figure. This will distribute the work among all the map nodes.
• Then, we tokenize the words in each of the mappers and give a hardcoded value (1) to each of the tokens or words. The rationale behind giving a hardcoded value equal to 1 is that every word will occur once.
• Now, a list of key-value pair will be created where the key is nothing, but the individual words and value is one. So, for the first line (Dear Bear River) we have 3 key-value pairs – Dear, 1; Bear, 1; River, 1. The mapping process remains the same on all the nodes.
• After the mapper phase, a partition process takes place where sorting and shuffling happen so that all the tuples with the same key are sent to the corresponding reducer.
• So, after the sorting and shuffling phase, each reducer will have a unique key and a list of values corresponding to that very key. For example, Bear, [1,1]; Car, [1,1,1] ..., etc.
• Now, each Reducer counts the values which are present in that list of values. As shown in the figure, reducer gets a list of values which is [1,1] for the key Bear. Then, it counts the number of ones in the very list and gives the final output as – Bear, 2.
• Finally, all the output key/value pairs are then collected and written in the output file.
33. How does MapReduce solve the problem of having a simplified model for distributed processing?
Ans:
MapReduce environment takes care of:
▪ Partitioning the input data
▪ Scheduling the program’s execution across a set of machines
▪ Performing the group by key step
▪ Handling machine failures
▪ Managing required inter-machine communication
34. In the case of Master worker failure, why does map tasks that have already been completed needs to be reset?
Ans:
Because, for map workers/ nodes, the intermediate outputs are stored on the local file system.
In case of Master failure:
- Client can instruct for master failure to be restarted
- However, the chance for master failure is highly unlikely. A typical server can last 1000 days.
35. Explain the need for having M map tasks and R reduce tasks that are larger than the number of nodes.
Ans:
In practice, it is more logical to have 1 map task per chunk
▪ One DFS chunk per map is common
▪ The main reason being it Improves dynamic load balancing and speeds recovery from worker failure
▪ And the map task is spread across the different nodes, just waiting to be assigned to available nodes when it becomes available
36. Produce MapReduce algorithms (in the form of a pseudo-code) to take a very large file of integers and produce as output: (a) The largest integer.
Ans:
map(key,value):
// key: file_id; value: list of integers
maxVal =0
for i in values:
if(i > maxVal):
maxVal = i
emit(key, maxVal)
reduce(key, values):
// key: file_id; values: list of maxVal
finalMaxVal = 0
for i in values:
if(i > finalMaxVal):
finalMaxVal = i
emit(‘MaxVal’, finalMaxVal)
(b) The average of all the integers.
Ans:
map(key, value):
// key: file _id: values: list of integers
sum = 0;
count = 0;
for i in value:
sum = sum + i
count = count + 1
emit(key, (sum,count)])
reduce(key, (sum,count)):
// key: file_id ; (sum,count): contains a list of sum & count pairs produced by each
// mapper task
sumTotal = 0
countTotal = 0
for (sumVal, countVal) in sum_count_list:
sumTotal = sumTotal + sumVal
counTotal = countTotal + countVal
average = sumTotal / countTotal
emit(‘AverageVal’, average)
(c) The count of the number of distinct integers in the input. Ans:
map(key, value):
# key: file_id: values: list of integers
for i in value:
emit(i,1)
reduce(key, ):
# key: file_id ; : contains a list of integers & 1 (denoting its occurrence)
#maps integers to their counts
int2count = {}
for ((i,1) in ):
int2count[i] = int2count.get(i,0) + 1
emit(int2count)
37. Explain the usage of triangular matrix and the two different methods to store the pair counts.
Ans:
The triangular matrix is used to store all the item pairs. Triangular matrix is for all values of items indices in which i is always lesser than j. For instance, the association rule i ⇒ j, all the i and j are stored where i < j. Two different methods to store the pair counts are triples and tabular method.
38. Briefly explain the main difference between A-Priori, PCY, Multi-Hash and Multi-Stage. Also provide the primary reason why the FP Growth algorithm is introduced.
Ans:
A-Priori is a technique to find frequent pairs without counting all pairs. It apply monotonicity concept, if a set of items appears at least s times, so does every subset. It can handle smaller datasets in main memory if comparing with PCY, Multi-Hash and Multi-Stage algorithm. It is designed to reduce the number of pairs that must be counted, at the expense of performing two passes over data.

The PCY Algorithm uses that space for an array of integers that generalizes the idea of a Bloom filter. The PCY algorithm also consists of two passes. The pass 1 has additional hash table for bucket counts compared to A-Priori Algorithm. In addition, the pass 2 also has additional bitmap.

The Multi-Stage algorithm improves upon PCY by using several successive hash table to reduce further the number of candidate pairs. Multi-stage algorithms can take more than two passes to find the frequent pairs. It might be obvious that it is possible to insert any number of passes between the first and last in the multistage Algorithm. The first pass of Multistage is the same as the first pass of PCY. But the second pass of Multistage does not count the candidate pairs. Rather, it uses the available main memory for another hash table, using another hash function. After the second pass, the second hash table is also summarized as a bitmap, and that bitmap is stored in main memory.

Sometimes, we can get most of the benefit of the extra passes of the Multistage Algorithm in a single pass. This variation of PCY is called the Multihash Algorithm. Instead of using two different hash tables on two successive passes, use two hash functions and two separate hash tables that share main memory on the first pass. The danger of using two hash tables on one pass is that each hash table has half as many buckets as the one large hash table of PCY.

FP Growth algorithm compresses data sets to a FP-tree, scans the database twice, does not produce the candidate item sets in mining process, and greatly improves the mining efficiency.
39a. Suppose there are 100 items, numbered 1 to 100, and also 100 baskets, also numbered 1 to 100. Item i is in basket b if and only if i divides b with no remainder. Thus, item 1 is in all the baskets, item 2 is in all fifty of the even-numbered baskets, and so on. Basket 12 consists of items {1, 2, 3, 4, 6, 12}, since these are all the integers that divide 12.
If the support threshold is 5, which items are frequent?
Ans:
Item 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20
39b. For the data mentioned in the previous question (i.e. Question 39a), what is the confidence of the following association rules?
(i) {5, 7} → 2.
Ans:
Basket 35, 70 consists of {5, 7}
Basket 70 consists of {5, 7, 2}
Confidence = ½ = 0.5
(ii) {2, 3, 4} → 5
Ans:
Basket 12, 24, 36, 48, 60, 72, 84, 96 consist of {2, 3, 4}
Basket 60 consist of {2, 3, 4, 5}
Confidence = 1/8 = 0.125
c. If we use a triangular matrix to count pairs, and n, the number of items, is 20, what pair’s count is in a[100]? Ans:
(7, 8) Hint: Refer to Section 6.2 (Market Baskets and the A-Priori Algorithm) of the Mining of Massive Datasets book with regards to the triangular matrix.
40. Apply the A-Priori algorithm to the data specified in Question 39a, with support threshold 5.
Ans:

More Free Exercises:
Data Science ExercisesBig Data Management Exercises
Principle in Data Science Exercises
Data Analytics Exercises
Data Mining Exercises
Network Security Exercises
Other Exercises:
Python String Exercises
Python List Exercises
Python Library Exercises
Python Sets Exercises
Python Array Exercises
Python Condition Statement Exercises
Python Lambda Exercises
Python Function Exercises
Python File Input Output Exercises
Python Tkinter Exercises

