Network Security - Exercises Section 1

1. What are the differences between passive attack and active attack?
Ans:
Passive attack has the nature of eavesdropping on, or monitoring of, transmission of information between the communicating parties, but does not modify of temper the message. It captures the message and may read the content. It can be used for traffic analysis e.g., who is a particular person communicating with and the frequency of communication. Active attack modifies a message stream or creates a false message. It is used to launch more severe form of attack.

2. Why are passive attacks difficult to detect and active attacks difficult to prevent?
Ans:
Passive attacks are very difficult to detect, because they do not involve any alteration of the data. Typically, the message traffic is sent and received in an apparently normal fashion, and neither the sender nor the receiver is aware that a third party has read the messages or observed the traffic pattern. Active attacks are quite difficult to prevent because of the wide variety of potential physical, software, and network vulnerabilities.

3. What are the shortcomings of key administration in symmetric encryption?
Ans:
i) Key Exhaustion
Symmetric Encryption suffers from behavior where every use of a key ‘leaks’ some information that can potentially be used by an attacker to reconstruct the key. The defenses against this behavior include using a key hierarchy to ensure that master or key-encryption keys are not over-used and the appropriate rotation of keys that do encrypt volumes of data. To be tractable, both these solutions require competent key-management strategies as if (for example) a retired encryption key cannot be recovered the data is potentially lost.
ii) Attribution data
Unlike asymmetric (public-key) Certificates, symmetric keys do not have embedded metadata to record information such as expiry date or an Access Control List to indicate the use the key may be put to - to Encrypt but not Decrypt for example. The latter issue is somewhat addressed by standards such as ANSI X9-31 where a key can be bound to information prescribing its usage. But for full control over what a key can be used for and when it can be used, a key-management system is required.
iii) Key Management at large scale
Where only a few keys are involved in a scheme (tens to low hundreds), the management overhead is modest and can be handled through manual, human activity. However, with a large estate, tracking the expiration and arranging rotation of keys quickly becomes impractical. Consider an EMV payment card deployment: millions of cards multiplied by several keys-per-card requires a dedicated provision and key-management system.

4. How many keys are required for two people to communicate via a symmetric cipher? How many keys are required for n people to communicate with each other securely?
Ans:
One secret key. n(n-1)/2 keys

5. Describe the Data encryption algorithm for 64-bit length plaintext and 56-bit length key of DES. Explain the decryption algorithm as well.
Ans:
The plaintext is 64 bits in length and the key is 56 bits in length; longer plaintext amounts are processed in 64-bit blocks. The DES structure is a minor variation of the Feistel network. There are 16 rounds of processing. From the original 56-bit key, 16 subkeys are generated, one of which is used for each round.

6. What are the drawbacks of DES that motivated the development of AES? Be very specific in your answer.
Ans:
1) short key length – subject to brute force attacks
2) short block length (64 bits) – not efficient
A third drawback is, perhaps, too many rounds and if 3DES needs to be used, the algorithm will become sluggish.


7. Message integrity protection failure is more prominent in stream cipher based encryption. Discuss in details with appropriate examples why this happens in a stream cipher.
Ans:
A stream cipher cannot protect message integrity because it is vulnerable to attacks in depth. For example, fund transfer messages are very highly structured. Suppose an attacker knew bytes 37-42 of such a message contained the amount to be transferred. They could request a modest sum (500 MYR) to be sent to an accomplice. If by wiretapping the attacker can obtain the corresponding ciphertext for the message C = M XOR K they know M for bytes 37-42 so know K for bytes 37-42.
They take the ciphertext and change bytes 37-42 to read 500,000 MYR XORed with K for bytes 37-42 then send it on. Mathematical prove:
C = Ciphertext, C1 = Modified ciphertext, K = key
C1 = C XOR (500 XOR 500,000)
Since C = 500 XOR K, the modified Ciphertext, C1 will be:
C1 = (500 XOR K) XOR (500 XOR 500,000)
= 500 XOR 500 XOR K XOR 500,000 - Associative Properties of XOR
= 0 XOR K XOR 500,000
= K XOR 500,000
At receipients, it will decrypt C1 XOR K
C1 XOR K = (K XOR 500,000) XOR K
= 500,000
Note that anything that XOR with it self will return 0, anything that XOR with 0 will return itself

8. Explain the error propagation of Ciphertext in Cipher Block Chaining Mode (CBC) and how does it affect the Plaintext.
Ans:
Let say there is an error in C1 (output of encryption in Block 1). But since C1 is input to the calculation of C2, C2 is affected. This effect carries through indefinitely, so that all ciphertext blocks are affected in encryption. However, at the receiving end, the decryption algorithm restores the correct plaintext for blocks except the one in error.

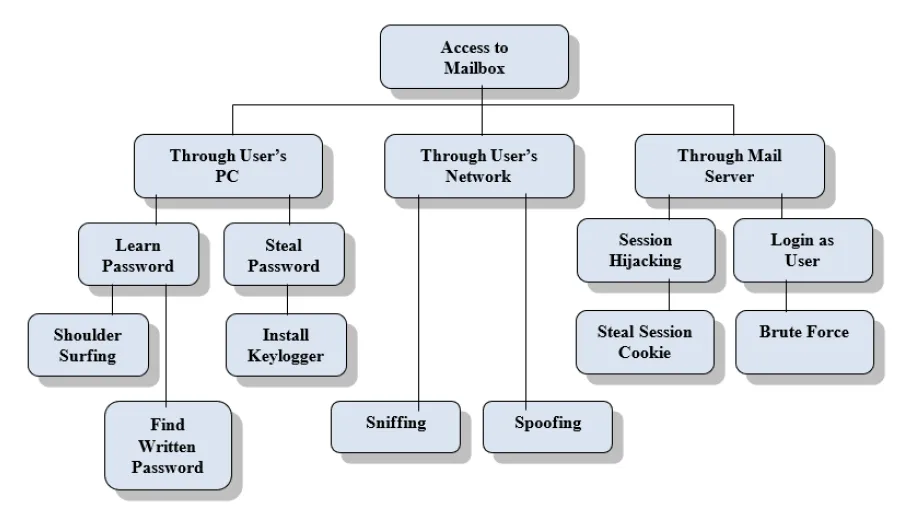
9. Develop an attack tree for gaining access to customer account details from the database of a bank.
Ans:
map

10. You are a junior IT executive at your department dealing with the DES encryption key. From the random key generator, you are given the secret key (E0E0E0E0F1F1F1F1)hex to encrypt a message.
i. What is the output of the key after it is applied with the parity bit drop process box in Figure 1? At this point, is it a strong or weak key? Please state your reason.
Ans:
(E0E0E0E0F1F1F1F1)hex conversion to binary:
K1 = (1110 0000 1110 0000 1110 0000 1110 0000 1111 0001 1111 0001 1111 0001 1111 0001)bin
After parity bit drop, or key initial permutation, or permutation compression (PC)
PC(K1) = (1111 1111 1111 1111 1111 1111 1111 0000 0000 0000 0000 0000 0000 0000)bin → 56
It seems like a weak key since it has predicted pattern, 1-28 bits are all 1 while the rest are all 0.

ii. Using the key-permutation compression 2 from Figure 2, decide whether this is a strong or weak key. Justify your answer.
map

Ans:
Take the input → IP(K1) = (1111 1111 1111 1111 1111 1111 1111 0000 0000 0000 0000 0000 0000 0000)
Break into two halves:
C0 = 1111 1111 1111 1111 1111 1111 1111
D0 = 0000 0000 0000 0000 0000 0000 0000
Circular left shift:
C1 = 1111 1111 1111 1111 1111 1111 1111
D1 = 0000 0000 0000 0000 0000 0000 0000 This will be input to round-1 key, K1
K1 = 1111 1111 1111 1111 1111 1111 1111 0000 0000 0000 0000 0000 0000 0000
Apply key-permutation compression (Figure 2) to 48-bits:
KPC(K1) = 1111 1111 1111 1111 1111 1111 0000 0000 0000 0000 0000 0000
This is a weak key, and if we continue next round until the final round, doing rotation and permutation will yield a same result (a predicted pattern of key), This is definitely a weak key.

11. Let M be the plaintext message M = MALAYSIA and the private key, K = ISSOGOOD
a) Convert this plaintext and key message to Hexadecimal representation using the ASCII table.
b) Convert the Hexadecimal representation to binary number.
c) Represent your plaintext binary number as a form of a block, using the DES encryption technique (2 equal blocks).
d) Using the initial permutation (table is provided below), please provide your plaintext output.
e) Using the expansion P-box (table is provided below), show the plaintext output of this process.
f) For the key: Using the key permutation table (provided below), show the output of this conversion process.
g) Using the appropriate steps of DES operation, what is the final output of the key for round 1 (hint: you have to use the circular left shift and permutation compression (PC) table provided below).
h) For round 1, please provide your output for the XOR operation of plaintext and the key, according to the DES operation.
i) Based on the output of 4(h), explain the next process using the S-box table, and show the output from this operation.
j) Based on the output of 4(i), explain the next process using a straight permutation table, and show the output from this operation.
1. PT: MALAYSIA
Ans:
a) (4d 41 4c 41 59 53 49 41)hex

b) PT = 0100 1101 0100 0001 0100 1100 0100 0001 0101 1001 0101 0011 0100 1001 0100 0001

c)
L0 = 11111111 00110000 00000101 11111011
R0 = 00000000 00000000 01010101 00100000

d) IP(M) = 11111111 00110000 00000101 11111011 00000000 00000000 01010101 00100000

e) Ln = Rn-1 Rn = Ln-1 + f(Rn-1,Kn)
L1 = R0 = 00000000 00000000 01010101 00100000
R1 = L0 + f(R0, K1)
Expand R0 to 48 bits using Expansion P-Box
E(R0) = 000000 000000 000000 000000 001010 101010 100100 000000
Key:
K: ISSOGOOD
a) K = (49 53 53 4F 47 4F 4F 44)hex
b) K = 01001001 01010011 01010011 01001111 01000111 01001111 01001111 01000100

f) KP(K) = 00000000 11111111 00000000 00000110 11101111 10000110 10010110

g) Rearrange in 7-bits per group
0000000 0111111 1100000 0000000 0110111 0111110 0001101 0010110
Rearrange left and right:
KL0 = 0000000 0111111 1100000 0000000
KR0 = 0110111 0111110 0001101 0010110
Using left shift table
KL1 = 0000000 1111111 1000000 0000000
KR0 = 1101110 1111100 0011010 0101100
Combine the left and right key:
KL1KR0 = 0000000 1111111 1000000 0000000 1101110 1111100 0011010 0101100
Using key permutation compression table:
PC (KL1KR0) = 10100000 10010010 01000010 00010011 11110010 11100111

h) XOR operation of E(R0) and PC (KL1KR0)
E(R0) = 00000000 00000000 00000000 00101010 10101001 00000000
PC(KL1KR0) = 10100000 10010010 01000010 00010011 11110010 11100111 E(R0) XOR PC(KL1KR0) = 10100000 10010010 01000010 00111001 01011011 11100111

i) Using S-Box
First we have to rearrange in 6-bits per group:
E(R0) XOR PC(KL1KR0) = 101000 001001 001001 000010 001110 010101 101111 100111
Applying sbox: 1101 1111 0011 1101 0110 1101 0111 0111

j) Using straight permutation table:
f = 11010110 10011110 11111100 11111110
R1 = L0 XOR f
---> 11111111 00110000 00000101 11111011 XOR
---> 11010110 10011110 11111100 11111110
---> 00101001 10101110 11111001 00000101
R1 = 00101001 10101110 11111001 00000101

12. Using the simplified RC4 Algorithm of 8 bytes (rather than the full 256 bytes), find the final Keystream and Cipherpext of the following Input string:
S-Array of length 8, [S0 S1 S2 S3 S4 S5 S6 S7] = [0 1 2 3 4 5 6 7]
Key, K = [3 1 4 1 5]
Plaintext, PT = [6 1 5 4]

Hint: For the simplified stream generation, you can use this pseudocode (only up to the PT length):

/* Initialization */
set i and j = 0
for i = i + 1 to length of PT
  j = j + S[i] mod 8
  swap S[i], S[j]
  t = S[i] + S[j] mod 8
  Keystream = S[t]
end for
Ans:
CT = PT XOR KeyStream
PT = CT XOR KeyStream
keylen = 8
[K0 K1 K2 K3 K4] = [3 1 4 1 5]
First Step is Initialization:
1. /* Initialization */
for i = 0 to 8 do
S[i] = i;
T[i] = K[i mod keylen]
T[i] is the new K[i]
The K array thus is [K0, K1, K2, K3, K4, K5, K6, K7] = [3, 1, 4, 1, 5, 3, 1, 4]

2. The next step:
/* Initial Permutation */
j = 0
for i = 0 to 7 do
  j = j + S[i] + K[i] mod 8
  swap S[i] and S[j]
end for K[0]= 3, K[1]= 1, K[2]= 4, K[3]= 1, K[4]= 5, K[5]= 3, K[6]= 1, K[7]= 4
map

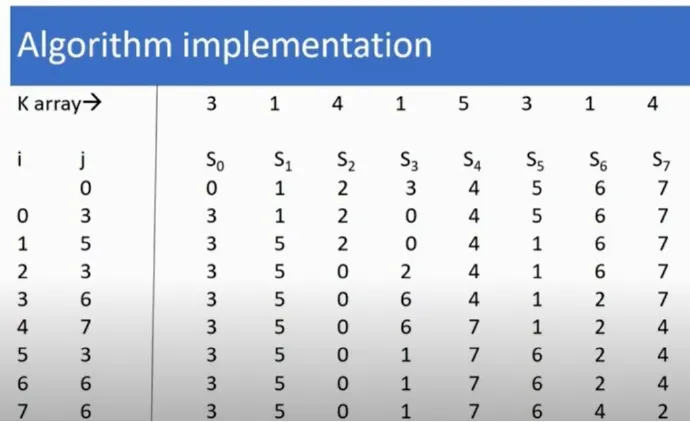
Resulting in (final row):
The new S-Array then becomes
[3 5 0 1 7 6 4 2]
3. Next, a simplified stream generation:
/* Simplified Stream Generation */
set i and j back to 0
for i = i + 1 to length of PT
  j = j + S[i] mod 8
  swap S[i] and S[j]
  t = S[i] + S[j] mod 8
  KeyStream = S[t]
end for
Will result in:

map

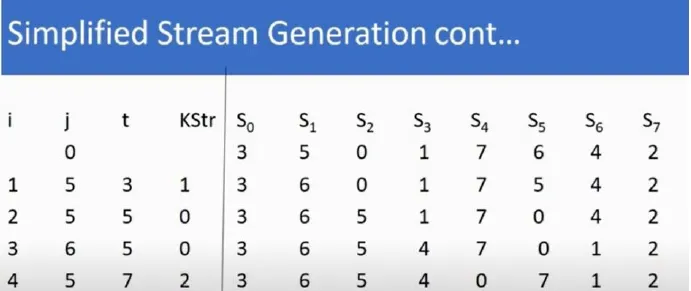
Final Keystream: K = S[t] = [1 0 0 2]
Plaintext: PT = [6 1 5 4]
CT = PT XOR K
CT = [0110 0001 0101 0100] XOR [0001 0000 0000 0010]
CT = 0111 0001 0101 0110 = [7 1 5 6]

13. Would it be possible to execute encryption functions in parallel on CBC mode with multiple blocks of messages? How about Decryption?
Ans:
In CBC decryption, the input blocks for the inverse cipher function (i.e., the ciphertext blocks) are immediately available, so multiple inverse cipher operations can be performed in parallel.
In CBC encryption, however, the input block to each forward cipher operation (except the first) depends on the result of the previous forward cipher operation, so the forward cipher operations cannot be performed in parallel.

14. Why Should the IV in CBC be protected?
Ans:
There are several reasons for protecting the IV. For instance, if an opponent is able to fool the receiver into using a different value for IV, then the opponent is also able to invert selected bits in the first block of plaintext. To see this, consider the following:
C1 = E(K, [IV @ P1])
P1 = IV @ D(K, C1)
Now use the notation that X[i] denotes the ith bit of the b-bit quantity X (b is the length of the block). Then:
P1[i] = IV[i] @ D(K, C1)[i]
Then, using the properties of XOR, we can state
P1[i]’ = IV[i]’ @ D(K, C1)[i]
Where the prime notation denotes bit complementation. This means that if an opponent can predictably change bits in IV, the corresponding bits of the received value of P1 can be changed.
In conclusion, because of the chaining mechanism of CBC, it is an appropriate mode for encrypting message of length greater than b bits

15. Differentiate between public-key cryptosystem and symmetric encryption algorithm.
Ans:
Public-key algorithms are based on mathematical functions rather than on simple operations on bit patterns, such as are used in symmetric encryption algorithms. Public-key cryptography is asymmetric, involving the use of two separate keys—in contrast to the symmetric conventional encryption, which uses only one key.

16. List the public key cryptography algorithm used in digital signatures, encryption/encryption and key exchange.
Ans:
map

17. What is a one-way hash function? How is it different from message authentication code?
Ans:
A one-way hash function, also known as a message digest, fingerprint or compression function, is a mathematical function which takes a variable-length input string and converts it into a fixed-length binary sequence. Furthermore, a one-way hash function is designed in such a way that it is hard to reverse the process, that is, to find a string that hashes to a given value (hence the name one-way.) A good hash function also makes it hard to find two strings that would produce the same hash value. As with the message authentication code, a hash function accepts a variable-size message M as input and produces a fixed-size message digest H (M) as output. Unlike the MAC, a hash function does not take a secret key as input. To authenticate a message, the message digest is sent with the message in such a way that the message digest is authentic.

18. What are a digital signature and a digital certificate?
Ans:
A digital Signature is an authentication mechanism that enables the creator of a message to attach a code that acts as a signature. The signature is formed by taking the hash of the message and encrypting the message with the creator's private key. The signature guarantees the source and integrity of the message.
Digital certificate binds an identity to a pair of keys that can be used to encrypt & sign digital information. It makes it possible for anyone to verify claims from individuals that they have the right to use a given key.

19. What is a public-key certificate?
Ans:
A public-key certificate consists of a public key plus a User ID of the key owner, with the whole block signed by a trusted third party. Typically, the third party is a certificate authority (CA) that is trusted by the user community, such as a government agency or a financial institution.

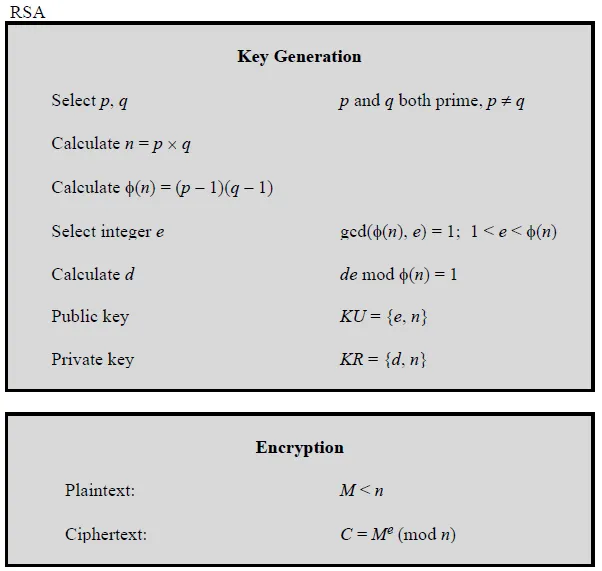
20. Briefly describe RSA and Diffie-Hellman operation.
Ans:
Diffie Helman
- A and B share a common prime number q and a, such that a < q and a is a primitive root of q
- A generates a private key XA such that XA < q, and B generates a private key XB such that XB < q
- A calculates a public key YA = a^XA mod q, and B calculates a public key YB = a^XB mod q
- A receives B’s public key YB in plaintext, and B receives A’s public key YA in plaintext
- A calculates shared secret key K = (YB)^XA mod q and B calculates shared secret key K = (YA)^XB mod q

map

map

21. List three approaches to message authentication
Ans:
Message encryption, message authentication code, hash function.




  1   2   3   4